详解快速排序
荷兰国旗问题
问题描述
拿破仑席卷欧洲大陆之后,代表自由,平等,博爱的竖色三色旗也风靡一时。荷兰国旗就是一面三色旗(只不过是横向的),自上而下为红白蓝三色。该问题本身是关于三色球排序和分类的,由荷兰科学家 Dijkstra 提出。由于问题中的三色小球有序排列后正好分为三类,Dijkstra 就想象成他母国的国旗,于是问题也就被命名为荷兰旗问题(Dutch National Flag Problem)。下面是问题的正规描述: 现有 n 个红白蓝三种不同颜色的小球,乱序排列在一起,请通过两两交换任意两个球,使得从左至右,依次是一些红球、一些白球、一些蓝球。在算法中,更多这样描述:如何通过两两交换,将一个数组中小于 N 的数放在靠左边,等于 N 的数放在靠中间,大于 N 的数放在靠右边 ;比如,数组 arr[1, 14, 5, 16, 8, 7], N=8, 则两两交换后得到[1, 7, 5, 8, 16, 14]。注意,左右两边内部不一定有序 。
问题分析
设计一个大(右)小(左)区间,通过不断扩展区间达到 分区(partition) 的效果。过程图示如下:
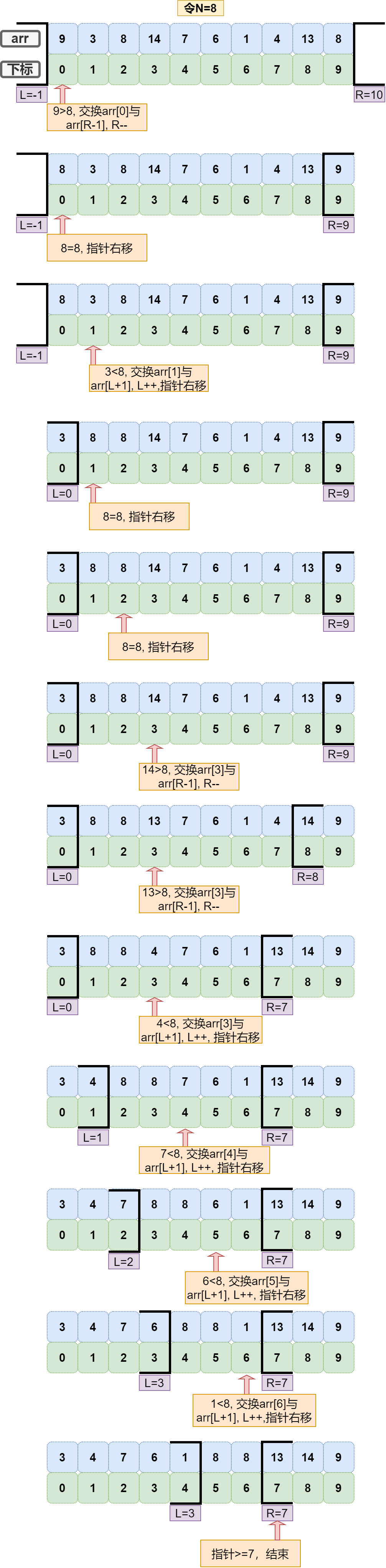
有以下几点需要注意:
- 左区间的初始位置为 L=-1,右区间的初始位置为 R=size;
- 当指针(下标为T)指向的数
-
小于 N 时:交换 arr[T] 和 arr[L+1] ,L++ ,T++;
-
等于 N 时,T++;
-
大于 N 时,交换 arr[T] 与 arr[R-1],R–,不可 T++ !
-
- T >= R 时,过程结束。注意,结束条件不能设置为 T==R,因为 R–,T++,可能有 T-R=1
- 区间内部不保证有序
代码实现
void netherLandFlag(int* arr, int size, int N)
{
int L = -1;
int R = size;
int T = 0;
while (T < R)
{
if (arr[T] < N)
swap(arr[T++], arr[++L]);
else if (arr[T] == N)
T++;
else
swap(arr[T], arr[--R]);
}
}
快速排序1.0
快速排序的核心就是递归调用荷兰国旗方法 。由于一旦完成 partition,中间区间(等于N的数)就不会再移动,所以就能通过不断在左右区间内部继续划分区间,直到无法划分为止,最终达到排序的效果 。在快速排序中,N 并不是上述那样人为指定的,而是固定为当前区间中最左或最右边的那个数 。如下图:
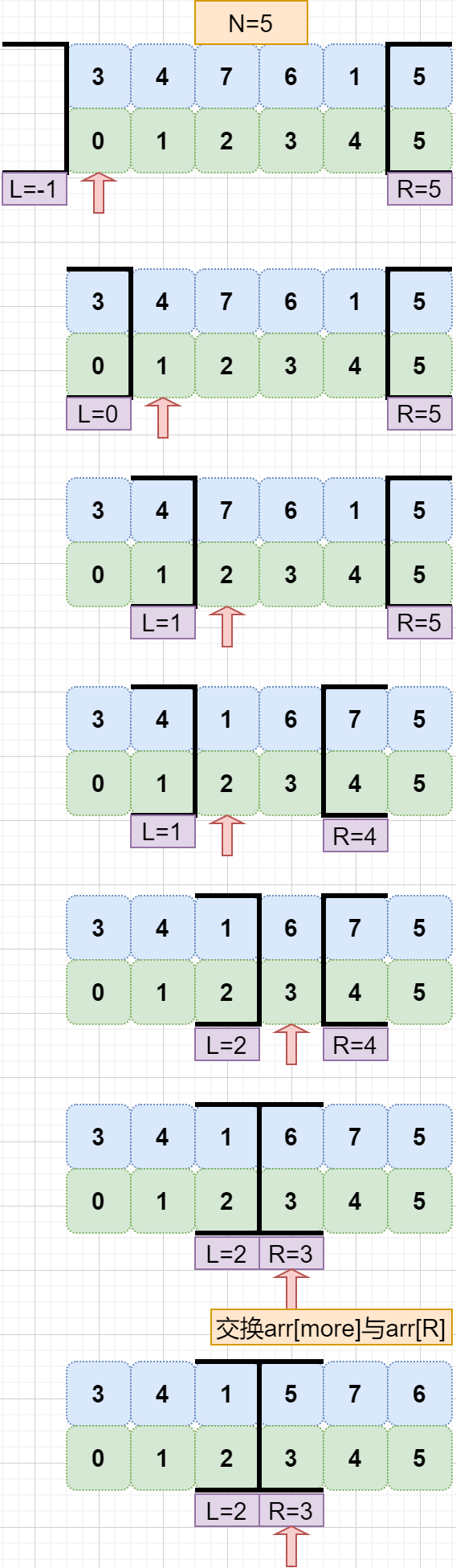
代码实现
// netherLandFlag 用于将数组划分为小于、等于和大于某个给定值 N 的部分
void partition(int* arr, int lower, int upper, int& pivotLow, int& pivotHigh) {
int L = lower - 1;
int R = upper + 1;
int T = lower;
int pivot = arr[lower]; //将该分区的首元素作为枢纽
while (T < R) {
if (arr[T] < pivot)
swap(arr[T++], arr[++L]);
else if (arr[T] == pivot)
T++;
else
swap(arr[T], arr[--R]);
}
pivotHigh = R - 1;
pivotLow = L + 1;
}
// 快速排序实现
void quickSort(int* arr, int lower, int upper) {
if (lower >= upper)
return;
int pivotLow, pivotHigh;
partition(arr, lower, upper, pivotLow, pivotHigh);
quickSort(arr, lower, pivotLow - 1);
quickSort(arr, pivotHigh + 1, upper);
}
快速排序2.0——随机快排
阅读上文后,读者也许能敏锐地发现,区间的划分情况和 N 息息相关。我们希望,N 总是可以打到数组的中间(数值, 而非位置),这样每次划分就可以达到类似于二分的效果;而一旦数组偏有序,那么划分次数就会大大增加 ,如下:
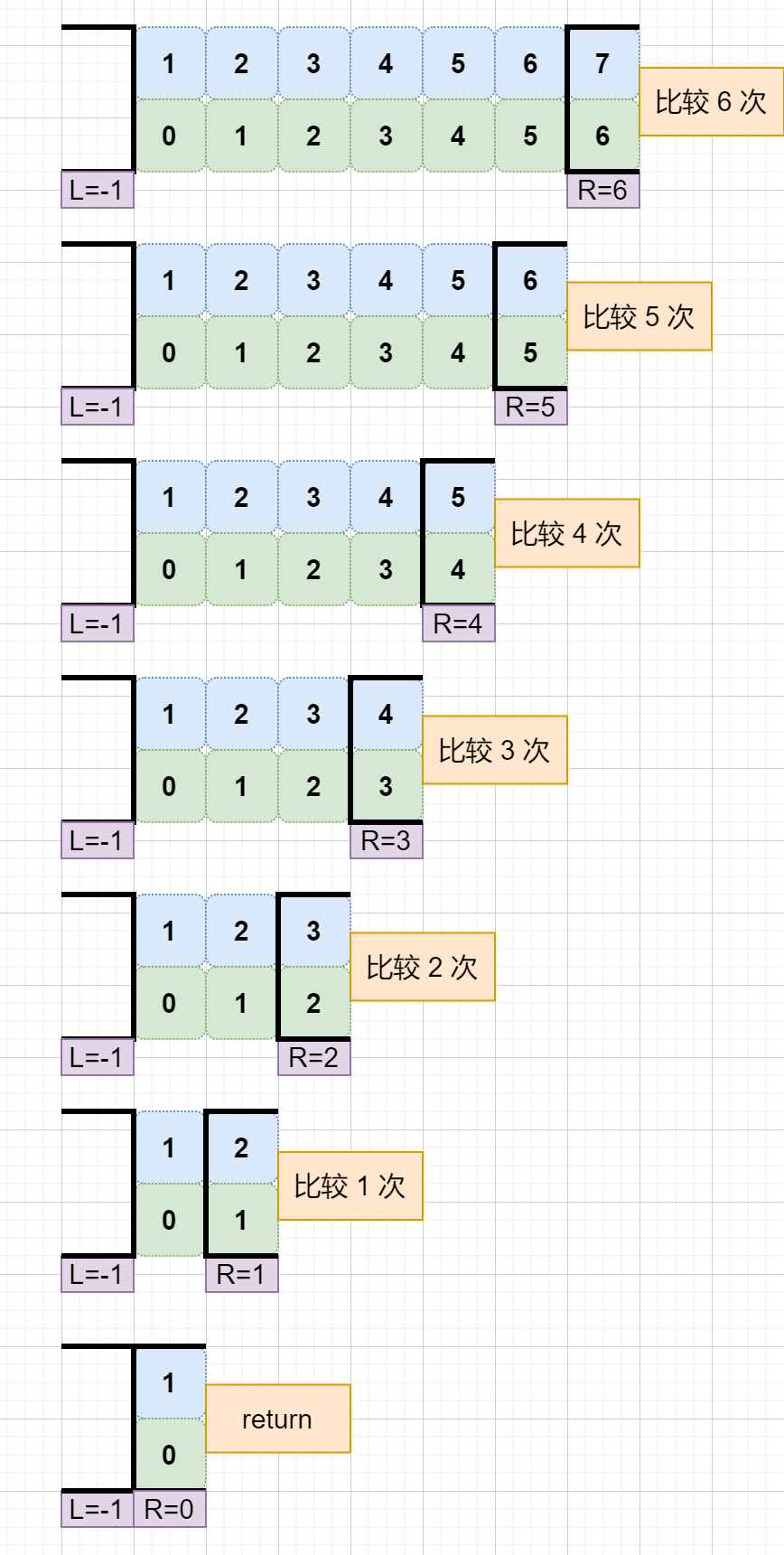
第 K 层比较次数为 N-K 次,笼统记为 N 次( 只要与 N 线性相关,都记为 N );一共 N-1 层,笼统记为 N 层;所以时间复杂度为 O(N^2) 。
如果每次打到中间,就可以产生二分效果,减少划分次数,如下:
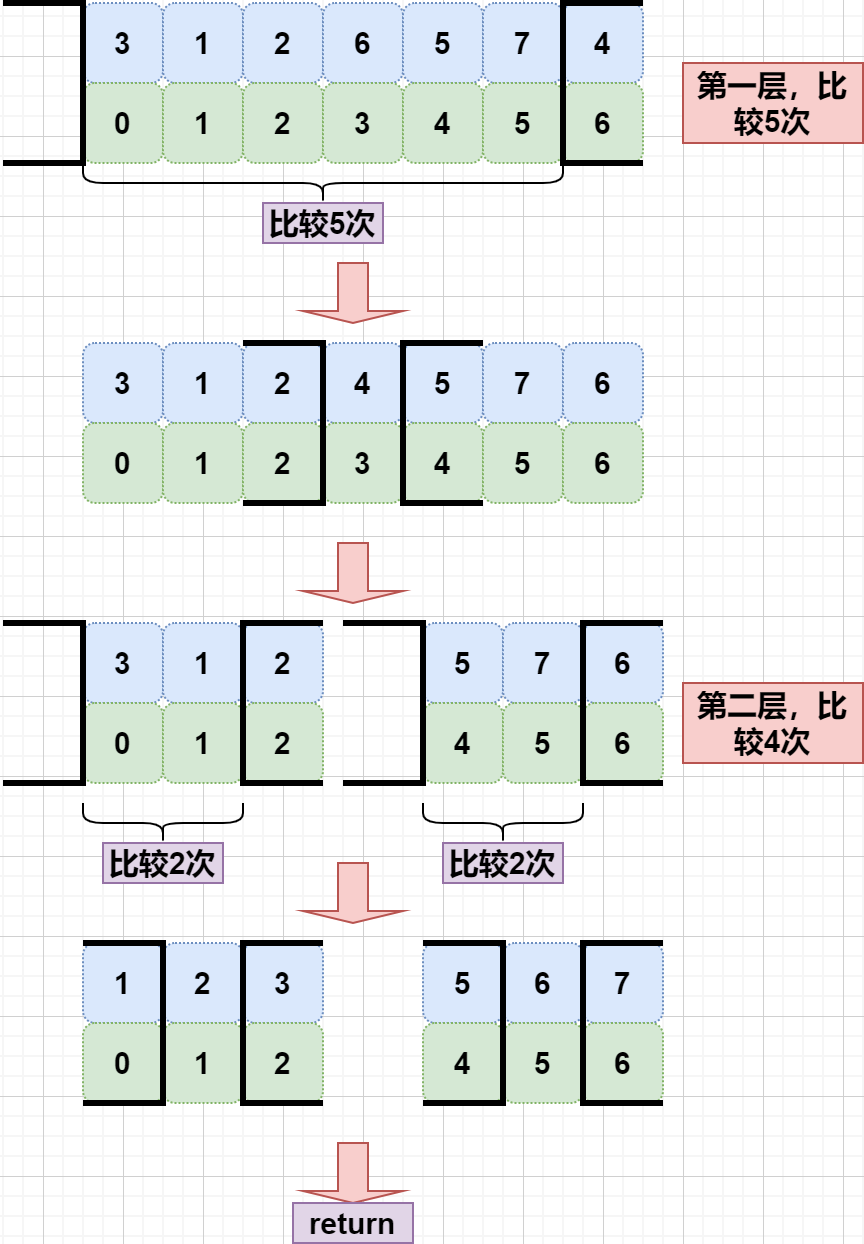
第 K 层比较次数为 N-K 次,笼统记为 N 次;一共有 log_2N 层( log_27=2 ),笼统记为 logN ,故时间复杂度为 NlogN 。
那么如何使 N 刚好打到数组的数值正中间呢?遗憾的是,无法做到,只能随机取值。但好消息是,将 N 随机取值(其值必须为数组中的数)后,该算法的长期期望也可以达到 NlogN 。在最坏状况下则需要次 O(N^2) 比较,但这种状况并不常见。
代码实现
#include<iostream>
#include<cstdlib>//rand()
#include<ctime>//time()
#include<cstring>//memcpy()
#include<vector>
void partition(int* arr, int lower, int upper, int& pivotLow, int& pivotHigh) {
int L = lower - 1;
int R = upper + 1;
int T = lower;
int pivot = arr[rand() % (upper - lower + 1) + lower];//在该分区随机取pivot
while (T < R) {
if (arr[T] < pivot)
swap(arr[T++], arr[++L]);
else if (arr[T] == pivot)
T++;
else
swap(arr[T], arr[--R]);
}
pivotHigh = R - 1;
pivotLow = L + 1;
}
效率比较
测试次数time=10000 ,最大值max=1000000000 ,最大长度size=1000000 ,快速排序 1.0 反而快于随机快排 0.6203 ms原因不详哈哈 :

