归并排序及其三道加强习题
归并排序(Merge Sort) 是利用归并的思想实现的排序方法，该算法采用经典的 分治(divide-and-conquer) 策略将问题分成一些小的问题然后递归求解，即分而治之。
递归实现
图解：
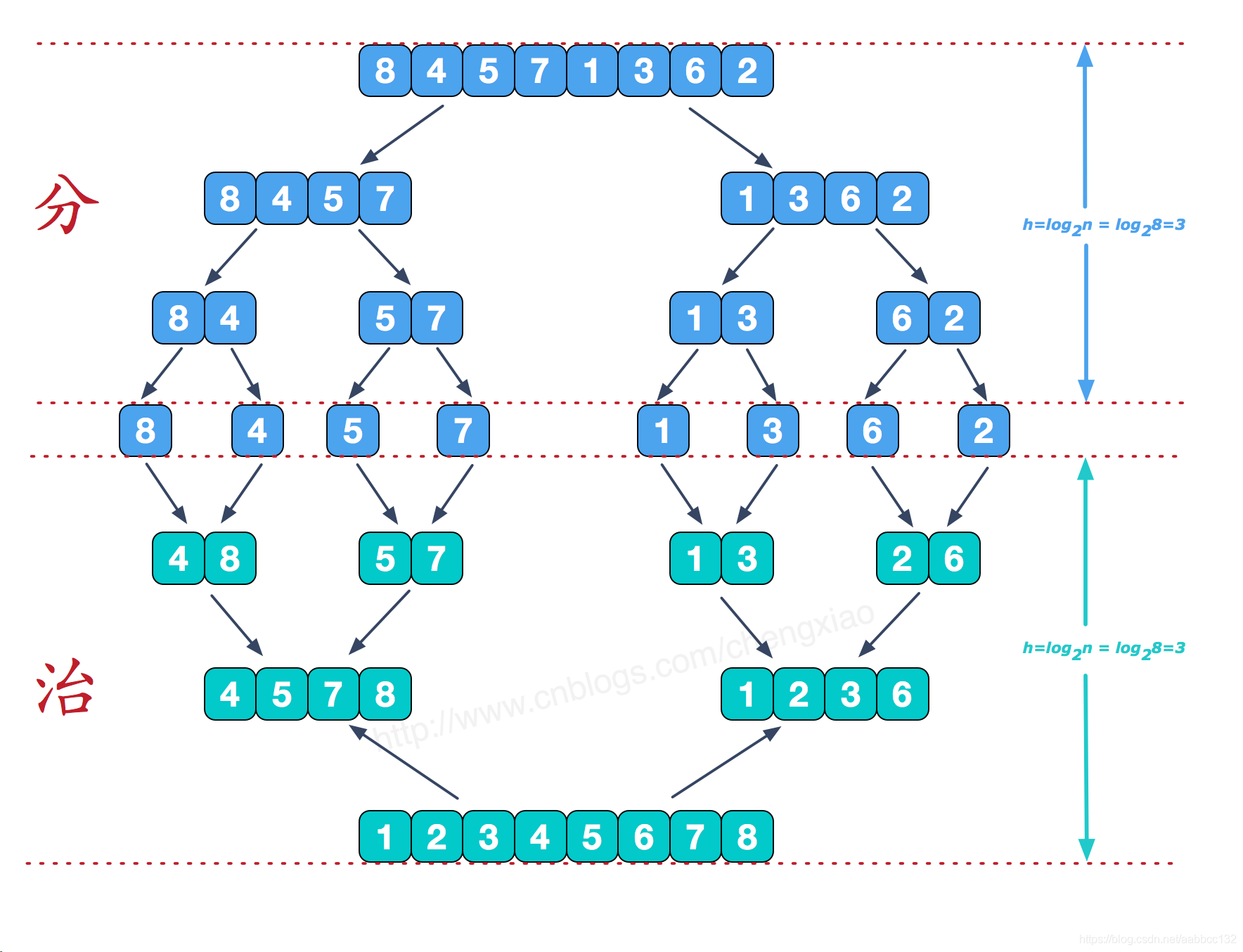
先递归将数组一分为二，直到不可再分；然后=依次将两边 合并(merge) ，合并的图解如下（以最后一次合并为例）：
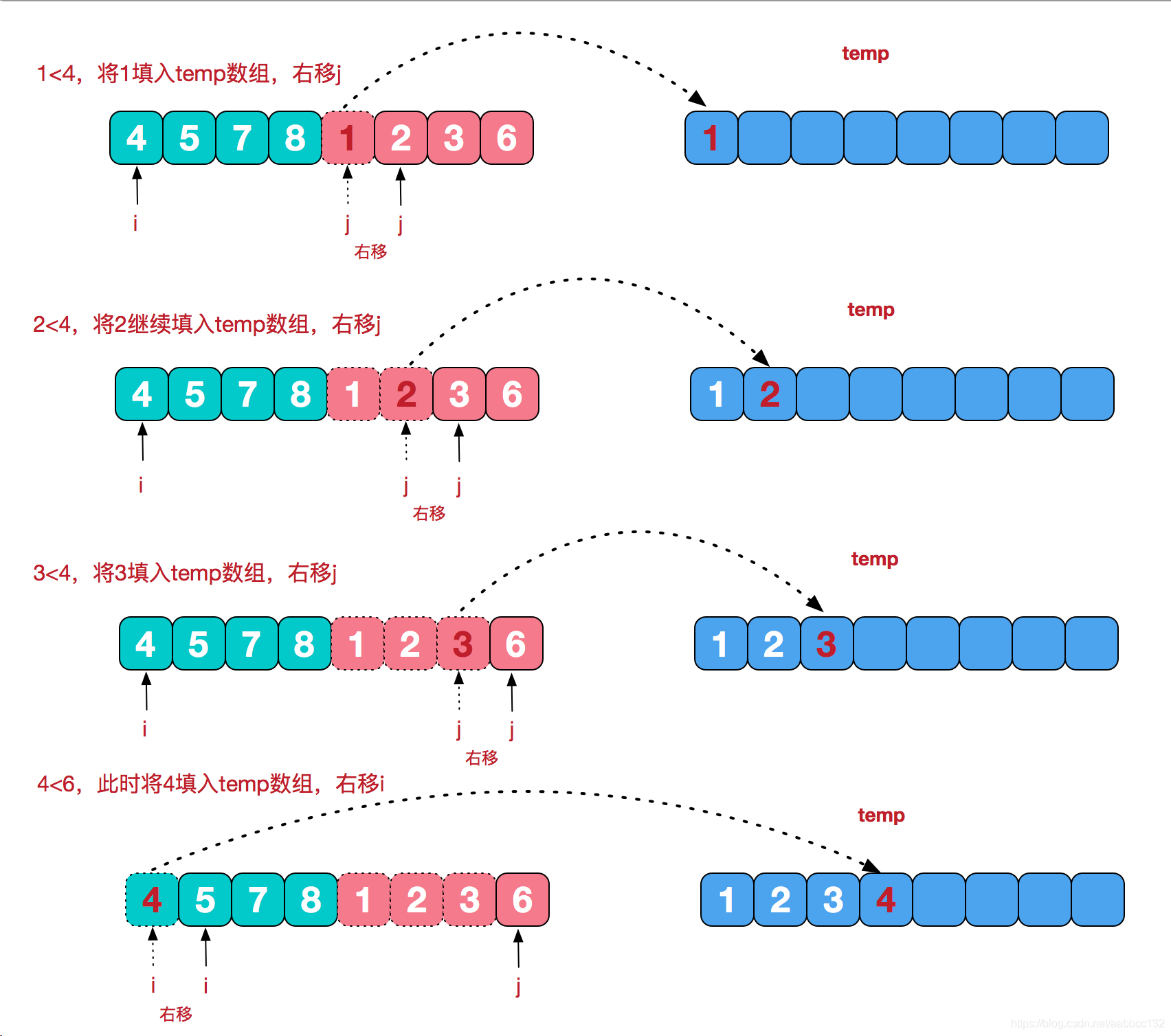
注意，之所以能这样合并，是因为两边的子数组都是已经排好序了的！而子数组最终也是通过该方法从单个元素排序而来 。从图可知，我们需要 new 一个辅助数组来存放左右两边比较后的结果；注意，当 i 移到 7 位置时，7>6，将 6 放入辅助数组，然后 j++，于是 j 超出数组范围，此时就直接将左半边余下的 7、8 放入辅助数组 ，结束。
void merge(int* vec, int* help, int l, int m, int r)
{
int p = 0;
int lp = l;
int rp = m + 1;
while (lp <= m && rp <= r)
help[p++] = (vec[lp] < vec[rp]) ? vec[lp++] : vec[rp++];
while (lp <= m)
help[p++] = vec[lp++];
while (rp <= r)
help[p++] = vec[rp++];
for (int i = 0; i < r - l + 1; i++)
vec[l + i] = help[i];
}
void process(int* vec, int* help, int l, int r)
{
if (l >= r)
return;
int m = (l + r) / 2;
process(vec, help, l, m);
process(vec, help, m + 1, r);
merge(vec, help, l, m, r);
}
// 归并排序主函数
void mergeSort(int* vec, int size)
{
if (size <= 1)
return;
int* help = new int[size];
process(vec, help, 0, size - 1);
delete[] help;
}
- 归并排序的边界条件很巧妙：[L，M]，[M+1，R] ，分到最后只剩一个元素时，就会有 L>=M，从而结束递归，比如所在区间：[0, 1]，L=0，R=1，M=(0+1)/2=0，左边进入递归 [0, 0]，右边进入递归 [1, 1]，自然就会满足基线条件(base case)，从而 return。对其他区间也同样如此。未来考虑某些边界条件时，这是一个很好的参考
- 注意 base case 是 l>=r 而非 l==r，左边界在某些情况下可能超过右边界，血的教训…
- 为什么 O(N^2) 这么 low ？因为它大量浪费了比较行为，前一次比较丝毫不能为以后的比较做出贡献。归并排序为什么好？因为它将每一次的比较结果都往后进行了传递，使后续的递归能够利用之前的比较成果
- 归并排序的复杂度为什么是 O(NlogN) ：因为最坏情况下，每一个数(即 N 个数)都会被比较 logN 次（递归层数）
- help数组每次都是被重复利用，后面merge会覆盖前面的merge，所以每次help使用完后无需清空。
迭代实现
归并排序的迭代实现也有较复杂的边界条件，笔者会用代码和示意图对应着解释这些边界。先上图：
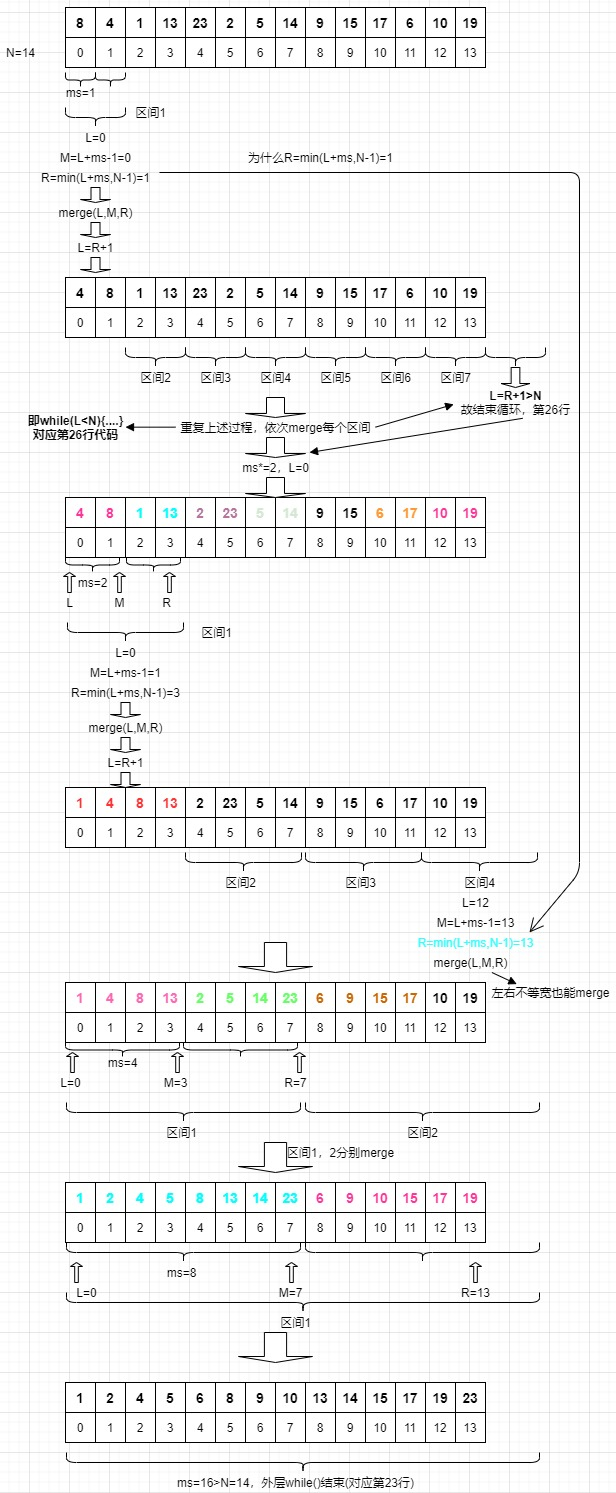
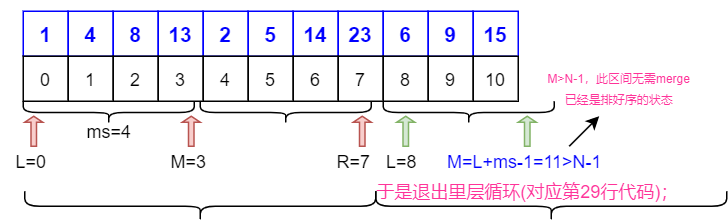
void merge(int* arr, int l, int m, int r)
{
int* help = new int[r - l + 1];
int p = 0;
int lp = l;
int rp = m + 1;
while (lp <= m && rp <= r)
help[p++] = arr[lp] < arr[rp] ? arr[lp++] : arr[rp++];
while (lp <= m)
help[p++] = arr[lp++];
while (rp <= r) //第9行和第10行的while只会进入其中一个
help[p++] = arr[rp++];
for (int i = 0; i < r - l + 1; i++)
arr[l + i] = help[i];
delete[] help;
}
void mergeSort(int* arr, int N)
{
if (arr == nullptr || N == 1)
return;
int mergeSize = 1, L, M, R;
while (mergeSize < N)
{
L = 0; //极易忽略
while (L < N)
{
M = L + mergeSize - 1;
if (M >= N-1) //极易忽略
break;
R = (M + mergeSize) < (N - 1) ? M + mergeSize : N - 1;
merge(arr, L, M, R);
L = R + 1;
}
if (mergeSize > N / 2)//防止整形溢出
break;
mergeSize *= 2;
}
}
int main()
{
int arr[] = { 1,23,24,51,3,56,27,17,10,43,25,36,86 };
mergeSort(arr, sizeof(arr) / sizeof(int));
for (int i = 0; i < sizeof(arr) / sizeof(int); i++)
{
cout << arr[i] << " ";
}
}
- 迭代实现的 merge() 与递归实现的 merge() 相同
- 第 25 行极易忽略！
- 第 28 到 31 行代码的顺序很容易记错，其位置不可颠倒！！！
- 重点要讨论的边界处理，即第 23、26、29 行代码，其理由已经在图中详细阐述。
- 第 35 行代码十分容易忽略。当 N 靠近整形边界时，mergeSize×2 就可能发生溢出成为负数，然后回到第 23 行进行比较，又重新进入 while 循环！所以未来在这种作了增加运算后还要和其他数进行比较时，须特别注意这类情况！
归并排序变式：三道面试题
小和问题
问题阐述
在一个给定的数组中，计算出每一个数左边的所有比其小的数的和，并将这些和相加，即得这个数组的小和。距离：对于数组 [6,3,8,9] ，6 的左边没有比 6 小的数；3 的左边没有比 3 小的数；8 的左边，6 和 3 小于 8，其和为 6+3=9；9 的左边，6，3，8 小于 9，其和为 17；故数组的小和为 26。
分析
显然，本问题可以很容易地被暴力破解，对每一个数，遍历之前的所有数，算法复杂度为 O(N^2) 。在暴力破解的基础上，我们会很容易地想到一些优化的方法，比如，当前数字为 7 时，往前挨个比较，当碰上数字 6 时，我们就可以停止遍历，直接将 6 和 6 的小和相加即可，如下图：
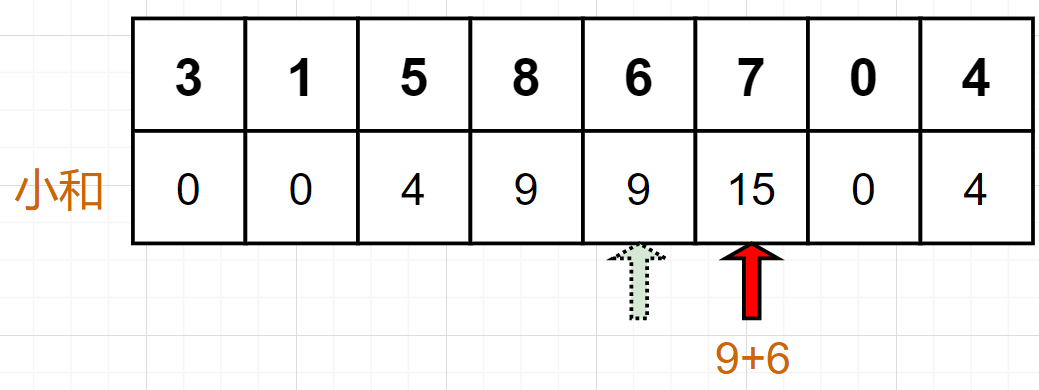
可见，当数字 N 左边紧挨着 N-1 时，此方式的效率就能达到最高；但如果碰上 [7,6,5,4,3,2,1] 这样从大到小的数列，复杂度也会回归到 O(N^2) 。那么，如何进一步优化？从以上过程可以隐约感受到，如果在求小和的过程中能够将之前比较过的数字由小到大进行排序，也许就可以充分利用上述优化方式。进一步，我们尝试引入归并排序（别问为什么，问就是不知道，呜呜呜）。仍然拿前文例子进行说明：
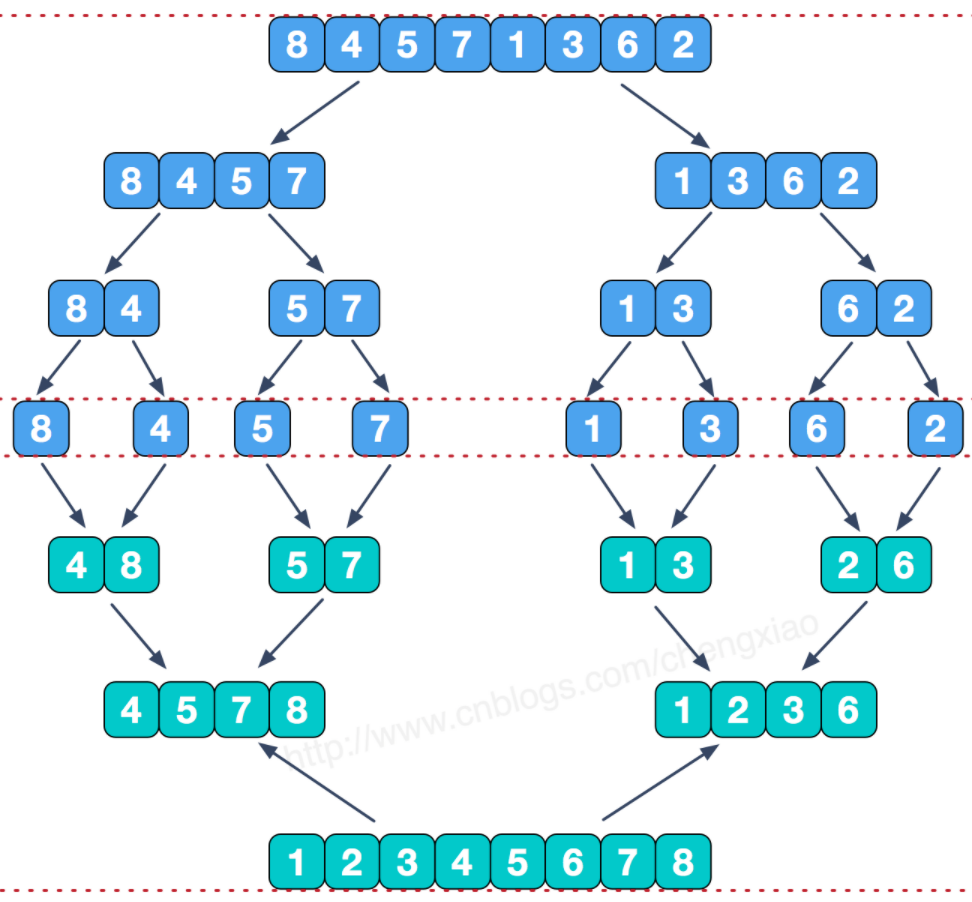
取出中间状态，分析步骤：
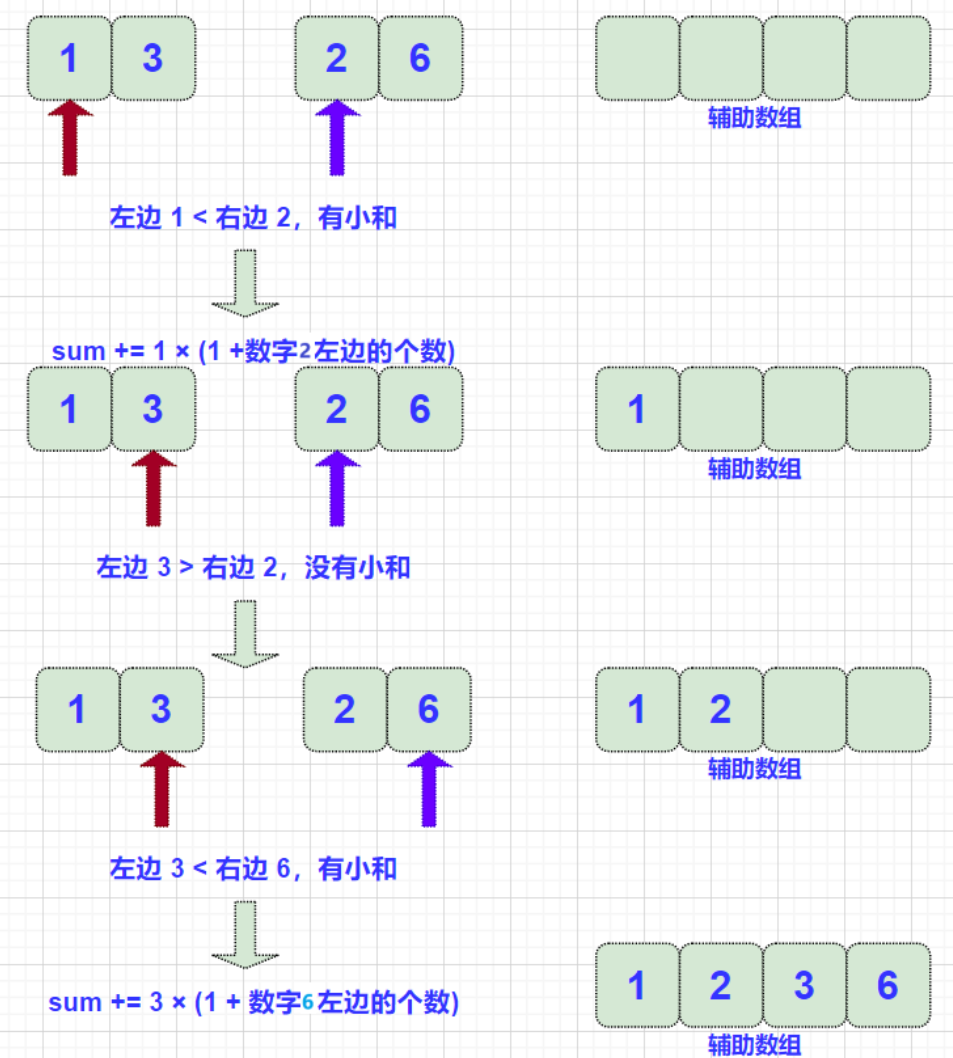
- 当有小和时，sum += 左边指向的数 × (右指针及其右边的数字个数) ，也即：sum += arr[lp] * (R - rp + 1) ；这是因为左右两组已经排好序的数组，例如 [2, 3, 4] 与 [3, 5, 9] merge 时，3 > 2 就能直接推出 3 后面的数都 > 2，因此直接 2 *(r-p2+1) 即可。 这是排序的最终用处。
- 此算法关键问题在于，为什么排序没有影响这些数字的小和？ 这是因为，在归并(merge)前，左组中的每一个数仍然在右组中每一个数的左边，这种状态并没有因为之前的排序而改变，直到本次merge才结束这种状态 。
- 此算法的代码实现，仅仅只改变了 merge() 函数（下面代码的第17-20行）
另外需要注意，当左边指针指向的数等于右边指针指向的数时，必须先将右边的数放入辅助数组！ 拿如下情况举例讲解：
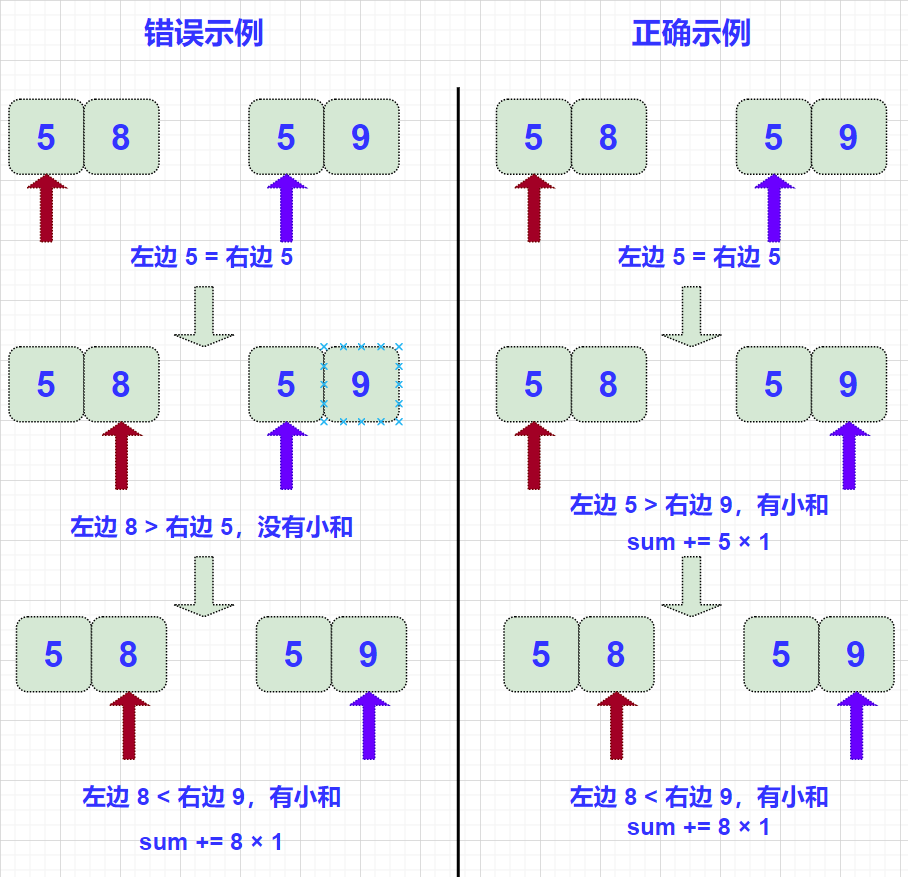
小和问题分析大致如此。代码如下：
#include<iostream>
#include<cstdlib>//rand()
#include<ctime>//time()
#include<cstring>//memcpy()
int count_1 = 0;
void merge(int* arr, int l, int m, int r)
{
int* help = new int[r - l + 1];
int p = 0; //help[]的pointer
int lp = l; //left pointer
int rp = m + 1; //right pointer
while (lp <= m && rp <= r)
{
if (arr[lp] < arr[rp])
{
count_1 += (r - rp + 1) * arr[lp];//
}
help[p++] = arr[lp] < arr[rp] ? arr[lp++] : arr[rp++];
}
while (lp <= m)
help[p++] = arr[lp++];
while (rp <= r) //第9行和第11行的while只可能进入一个
help[p++] = arr[rp++];
for (int i = 0; i < r - l + 1; i++)
arr[l + i] = help[i];
delete[] help;
}
void process(int* arr, int l, int r)
{
if (l == r)//base case
return;
int m = l + ((r - l) >> 1);
process(arr, l, m);
process(arr, m + 1, r);
merge(arr, l, m, r);
}
void mergeSort(int* arr, int size)
{
if (size == 1)
return;
int r = size - 1;
process(arr, 0, r);
}
逆序对问题
问题阐述
在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。
输入: [7,5,6,4]
输出: 5
逆序对：<7,5>,<7,6>,<7,4>,<5,4>,<6,4>
分析
同小和问题类似，都是左边的数比较右边的数，解决思路几乎相同，唯一不同是，需要从大到小排序！
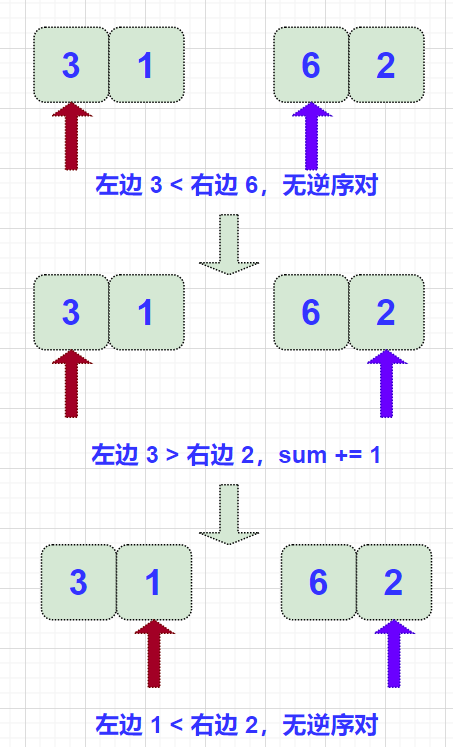对 merge() 稍作修改即可：
void merge(int* arr, int l, int m, int r)
{
int* help = new int[r - l + 1];
int p = 0; //help[]的pointer
int lp = l; //left pointer
int rp = m + 1; //right pointer
while (lp <= m && rp <= r)
{
if (arr[lp] > arr[rp])
{
count_1 += r - rp + 1;
}
help[p++] = arr[lp] > arr[rp] ? arr[lp++] : arr[rp++];
}
while (lp <= m)
help[p++] = arr[lp++];
while (rp <= r) //第9行和第11行的while只可能进入一个
help[p++] = arr[rp++];
for (int i = 0; i < r - l + 1; i++)
arr[l + i] = help[i];
delete[] help;
}
两倍大问题
给定一个数组，计算出每个数右侧比自身要小两倍还多的数的累计个数。如数组 [9,5,4,2] ，9 -> 4，9 ->2，5 -> 2，结果为 3。
分析
同逆序对类似，也是关于前面数字大于后面数字的问题，所以也最好使用归并算法的降序方式。 不同的是，此时不能一边 merge 一边比较二倍大 。如果仍按之前的方式边计算边 merge，会出现如下逻辑问题：
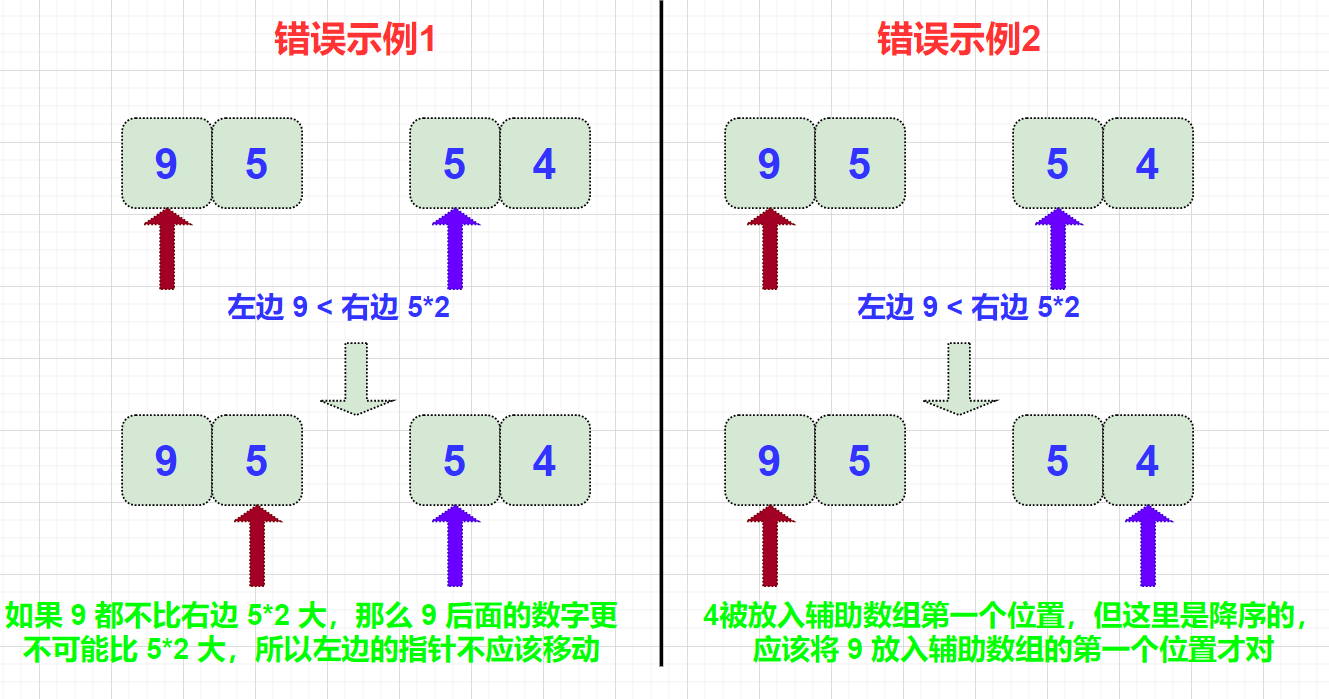
所以应该先完成所有计算，再 merge：
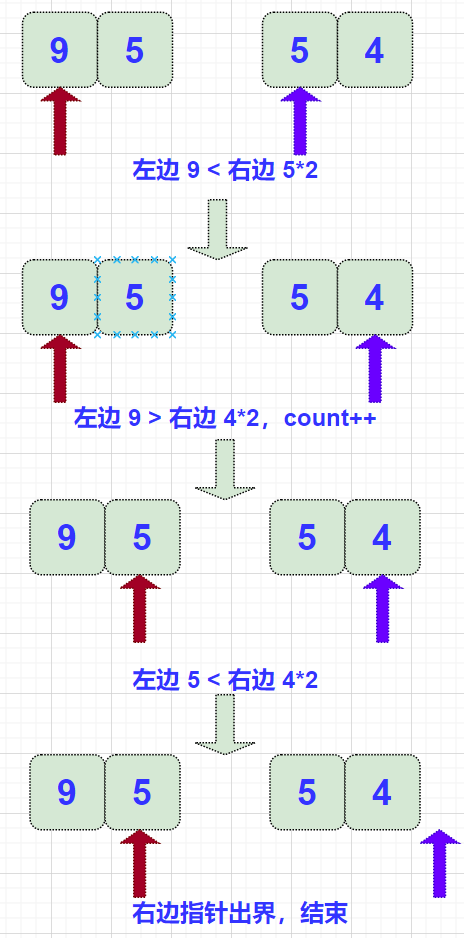
代码如下：
void merge(int* arr, int l, int m, int r)
{
int lp = l;
int rp = m + 1;
while (rp <= r && lp<=m)
{
if (arr[lp] > (arr[rp] * 2))
{
count_1 += r - rp + 1;
lp++;
}
else
rp++;
}
int* help = new int[r - l + 1];
int p = 0; //help[]的pointer
lp = l; //left pointer
rp = m + 1; //right pointer
while (lp <= m && rp <= r)
{
help[p++] = arr[lp] > arr[rp] ? arr[lp++] : arr[rp++];
}
while (lp <= m)
help[p++] = arr[lp++];
while (rp <= r) //第9行和第11行的while只可能进入一个
help[p++] = arr[rp++];
for (int i = 0; i < r - l + 1; i++)
arr[l + i] = help[i];
delete[] help;
}
总结
不难发现这三个问题的共同点：一个数组中，某个数的一侧，比它大或比它小的数…
归并排序能够解决此类问题的原因在于：在归并两个子数组前，左组中的每一个数仍然在右组中每一个数的左边，这种状态并没有因为之前的排序而改变，直到本次归并后才会改变这种状态。
因此解决类似的问题，都可以往归并上靠拢。